
❤️TensorFlow-Basic image classification
首先完整代码如下,接下来进行代码解析,并记录一些我学习到的地方。
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
print(tf.__version__, tf.config.list_physical_devices('GPU'))
fashion_mnist = tf.keras.datasets.fashion_mnist
(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()
print(train_images.shape, train_labels.shape)
class_names = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat', 'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']
train_images = train_images / 255.0
test_images = test_images / 255.0
plt.figure(figsize=(10, 10))
plt.imshow(train_images[0])
plt.colorbar()
plt.grid(False)
plt.show()
plt.figure(figsize=(10, 10))
for i in range(25):
plt.subplot(5, 5, i + 1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(train_images[i], cmap=plt.cm.binary)
plt.xlabel(class_names[train_labels[i]])
plt.show()
model = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=(28, 28)),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10)
])
model.compile(optimizer='adam', loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
model.fit(train_images, train_labels, epochs=10)
test_loss, test_acc = model.evaluate(test_images, test_labels, verbose=2)
print('Test accuracy:', test_acc)
probability_model = tf.keras.Sequential([model,
tf.keras.layers.Softmax()])
predictions = probability_model.predict(test_images)
print(predictions[0])
def plot_image(i, predictions_array, true_label, img):
true_label, img = true_label[i], img[i]
plt.grid(False)
plt.xticks([])
plt.yticks([])
plt.imshow(img, cmap=plt.cm.binary)
predicted_label = np.argmax(predictions_array)
if predicted_label == true_label:
color = 'blue'
else:
color = 'red'
plt.xlabel("{} {:2.0f}% ({})".format(class_names[predicted_label],
100 * np.max(predictions_array),
class_names[true_label]),
color=color)
def plot_value_array(i, predictions_array, true_label):
true_label = true_label[i]
plt.grid(False)
plt.xticks(range(10))
plt.yticks([])
thisplot = plt.bar(range(10), predictions_array, color="#777777")
plt.ylim([0, 1])
predicted_label = np.argmax(predictions_array)
thisplot[true_label].set_color('red')
thisplot[predicted_label].set_color('blue')
i = 1
plt.figure(figsize=(6, 3))
plt.subplot(1, 2, 1)
plot_image(i, predictions[i], test_labels, test_images)
plt.subplot(1, 2, 2)
plot_value_array(i, predictions[i], test_labels)
plt.show()
i = 12
plt.figure(figsize=(6, 3))
plt.subplot(1, 2, 1)
plot_image(i, predictions[i], test_labels, test_images)
plt.subplot(1, 2, 2)
plot_value_array(i, predictions[i], test_labels)
plt.show()
num_rows = 5
num_cols = 3
num_images = num_rows * num_cols
plt.figure(figsize=(2 * 2 * num_cols, 2 * num_rows))
for i in range(num_images):
plt.subplot(num_rows, 2 * num_cols, 2 * i + 1)
plot_image(i, predictions[i], test_labels, test_images)
plt.subplot(num_rows, 2 * num_cols, 2 * i + 2)
plot_value_array(i, predictions[i], test_labels)
plt.tight_layout()
plt.show()
img = test_images[1]
img = (np.expand_dims(img, axis=0))
print(img.shape)
predictions_single = probability_model.predict(img)
print(predictions_single)
plot_value_array(1, predictions_single[0], test_labels)
_ = plt.xticks(range(10), class_names, rotation=45)
plt.show()
np.argmax(predictions_single)1.Import the Fashion MINIST dataset
fashion_mnist = tf.keras.datasets.fashion_mnist
(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()Loading the dataset returns 4 NumPy arrays:
The train_images and train_labels arrays 是训练集(trainning set),用于训练模型
The test_images and test_labels arrays 是测试集(test set),用于测试模型
images 是 28 * 28 NumPy 数组,像素值在(0~255)。标签(label)是(0~9)的整数数组,对应关系如下:
2.Preprocessing the data
将数据值缩放(scale)到0~1的范围,然后再将其喂(feeding)给神经网络模型(neural network model)。训练集和测试集做相同的处理。
train_images = train_images / 255.0
test_images = test_images / 255.0那么为什么要这么处理呢?有以下几个原因
在标准的8位(bit)图像中,像素值(pixel value)是(0~255)
除以255.0是为了保持精度,毕竟是浮点数
保证像素的信息在归一化(Normalization)过程中不会丢失,使其更容易被激活函数(Activation Function)处理
统一数据范围和加速收敛(Convergence),优化器(Optimizer)(如SGD,Adam)在处理相似的数据时能更加有效,减少训练时间。
验证数据是否被正确格式化,显示其中的25张图片,并在图片下方显示标签。
plt.figure(figsize=(10,10))
for i in range(25):
plt.subplot(5,5,i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(train_images[i], cmap=plt.cm.binary)
plt.xlabel(class_names[train_labels[i]])
plt.show() 3.Build the model
3.Build the model
构建神经网络模型,需要配置模型的层(layer),然后编译(compiling)模型。
model = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=(28, 28)),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10)
])3.1此处出现了层,那么什么是层呢?
在神经网络中,**层(Layer)**是构成网络的基本结构单元。每一层由多个神经元(也称为节点)组成,层与层之间通过连接(权重)进行交互。不同层的作用和功能各不相同,通常可以分为以下几种类型:
输入层(input Layer)
功能:接收原始输入数据,并将其传递到网络的下一层。
组成:每个输入特征对应一个输入节点。输入层的节点数通常与特征数相同。
隐藏层(Hidden Layer)
功能:进行特征提取和变换,学习数据的表示。隐藏层可以是一个或多个,深度神经网络通常包含多个隐藏层。
组成:每个隐藏层的节点与上一层的所有节点相连接,节点之间通过激活函数实现非线性变换。
输出层(Output Layer)
功能:生成最终的预测或分类结果,输出对输入数据的表示。
组成:输出层的节点数通常与任务相关,例如,对于二分类任务通常有1个节点(使用sigmoid激活函数),而对于多分类任务则需使用多个节点(使用softmax激活函数)。
不同类型的层可以实现不同的功能,主要包括:
全连接层(Fully Connected Layer, FC Layer):每个节点与前一层的所有节点相连,常用于分类任务的输出层或隐藏层。
卷积层(Convolutional Layer):用于处理图像数据,通过卷积操作提取特征,能够有效捕捉局部特征。
池化层(Pooling Layer):用于减少数据维度,降低计算复杂度,同时提取主要特征(如最大池化、平均池化)。
递归层(Recurrent Layer):用于处理序列数据(如时间序列或自然语言处理),能够保留时间序列中的信息。常见的有长短期记忆(LSTM)和门控循环单元(GRU)。
正则化层(Regularization Layer):例如批量归一化(Batch Normalization)和dropout层,用于提高网络的稳定性和避免过拟合。
那么此处代码中出现的 tf.keras.layers.Flatten 和 tf.keras.layers.Dense属于什么层呢?
Flatten属于 转换层(Transformation Layer)。它的主要功能是将输入的多维张量(如图像数据)展平为一维张量。
Dense是 TensorFlow Keras 中的一种 全连接层(Fully Connected Layer),也称为 密集层(Dense Layer)。它是深度学习模型中最常用的层之一,主要用于执行线性变换和非线性激活操作。
线性变换: Dense层对输入进行线性变换,即将输入向量与权重矩阵进行点乘,并加上偏置项。
激活函数:可以使用非线性激活函数(如 ReLU、Sigmoid、Softmax 等)对输出进行处理,帮助模型学习非线性关系。
3.2此处还有一个激活函数,它又是什么呢?
激活函数是神经网络中的一个重要组件,它决定了神经元的输出。激活函数的主要作用是引入非线性因素,使得神经网络能够学习和表示复杂的模式和关系。没有激活函数,深度神经网络将只能表示线性组合,限制了其表现能力。
常见的激活函数包括:
Sigmoid 函数\sigma(x) = \frac{1}{1 + e^{-x}}:输出范围在0到1之间,适用于二分类问题,但在输入值较大或较小时容易出现梯度消失。
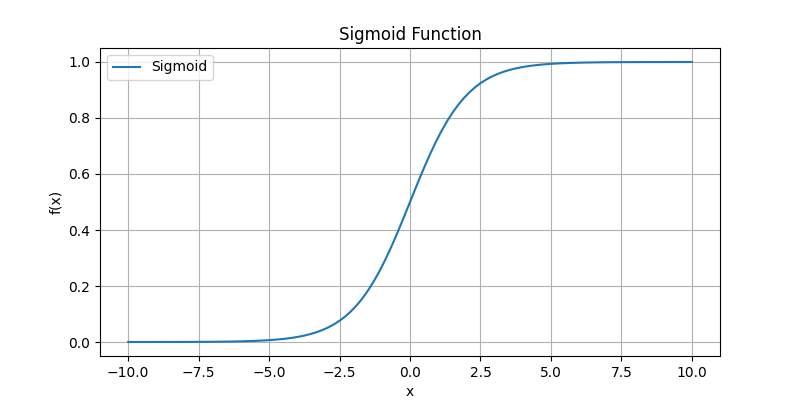
Tanh 函数\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}:输出范围在-1到1之间,比Sigmoid函数更为有效,且对输入值的平均值进行了中心化。
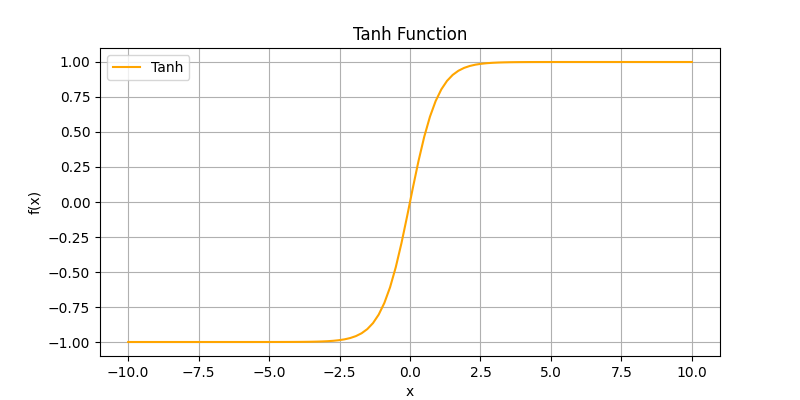
ReLU(Rectified Linear Unit)f(x) = \max(0, x):输出为输入值和0中的较大者,是当前最常用的激活函数之一,计算简单且在一定程度上缓解了梯度消失的问题。但在负数部分,输出为0,可能导致“死亡神经元”现象。
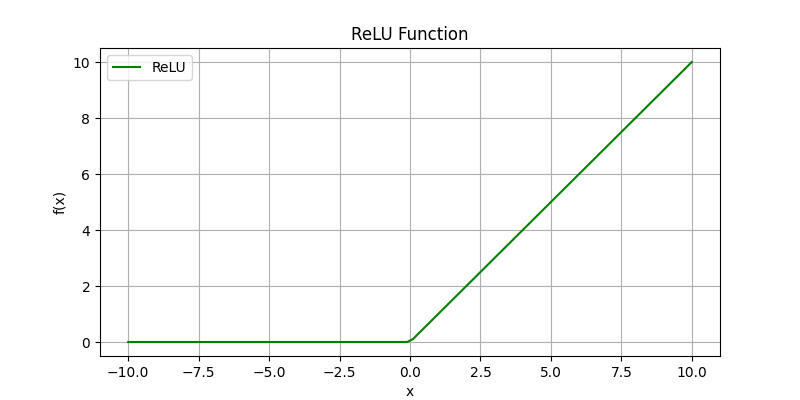
Leaky ReLU f(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha x & \text{if } x \leq 0 \end{cases}:是ReLU的一个变种,允许在负数区域有一个小的斜率,以避免“死亡神经元”问题。
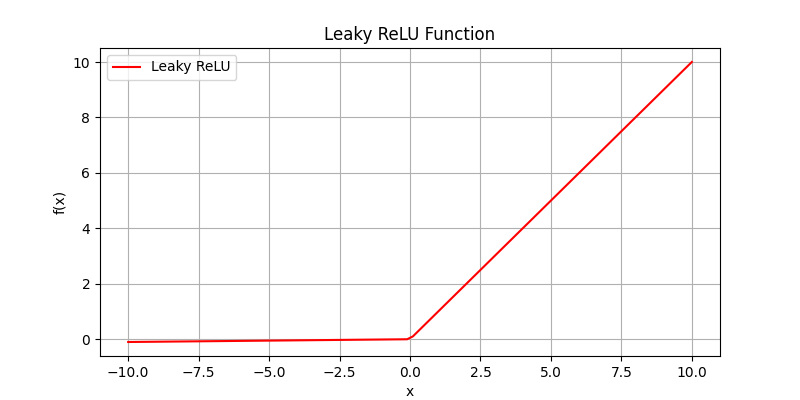
这里 αα 是一个小常数。
Softmax 函数 \text{Softmax}(z_i) = \frac{e^{z_i}}{\sum_{j} e^{z_j}}:常用于多分类问题的输出层,将输出转换为概率分布。
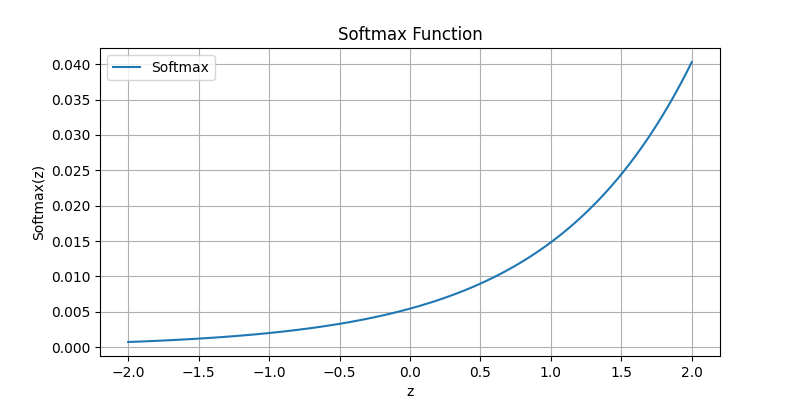
选择合适的激活函数是构建高效神经网络的关键之一,不同的激活函数可以影响模型的收敛速度和最终性能。
4.Compile the model
model.compile(optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])此处出现了几个新概念优化器(Optimizer),损失函数(Loss Function),和评估指标(Evaluation Metrics),它们是什么呢?
4.1优化器(Optimizer)
优化器:优化器是用于训练机器学习模型,特别是深度学习模型的一种算法或方法。它的主要职责是通过调整模型中的参数(例如权重和偏置)以最小化损失函数,从而提高模型的性能。
优化器的工作原理:
损失函数:
在训练过程中,模型根据输入数据做出预测,然后根据真实标签计算损失值。损失函数可以是均方误差、交叉熵等。
计算梯度:
优化器利用反向传播算法计算损失函数相对于模型参数的梯度(梯度是损失函数在参数空间中变化的方向和幅度)。这告诉优化器在参数空间中如何移动以减少损失。
调整参数:
根据计算得出的梯度和学习率(一个超参数,用于控制每次更新的步幅大小),优化器更新模型参数。常见的参数更新公式为:
θ=θ−α⋅∇L(θ)θ=θ−α⋅∇L(θ)
其中,θθ 是参数,αα 是学习率,∇L(θ)∇L(θ) 是损失函数对参数的梯度。
常用的优化器如下:
SGD (Stochastic Gradient Descent):
传统的随机梯度下降法,每次迭代中用一个样本或小批量的样本计算梯度,并更新参数。
可选的动量(momentum)技术可以加速收敛并减少震荡。
Momentum:
在 SGD 的基础上,添加了动量项,旨在加速收敛并减小震荡。它通过在参数更新中引入上一步更新的影响来实现。
Nesterov Accelerated Gradient (NAG):
基于动量的改进,在更新参数之前,先计算前一步的梯度,也就是进行“预见性”更新,通常能够获得更快的收敛速度。
AdaGrad (Adaptive Gradient Algorithm):
针对稀疏梯度问题进行改进,自动调整每个参数的学习率,学习率在训练过程中逐渐减小,更加关注于稀疏特征。
RMSprop:
针对 AdaGrad 的缺点进行了改进,通过引入指数衰减平均来调整学习率,从而解决了学习率过早减小的问题。
Adam (Adaptive Moment Estimation):
结合了 AdaGrad 和 RMSprop 的优点,使用动量和自适应学习率,通常在多种任务中效果良好,是当前最流行的优化器之一。
AdaDelta:
对 AdaGrad 的进一步改进,避免了学习率的急剧减小,通过限制过去梯度的影响来动态调整学习率。
FTRL (Follow The Regularized Leader):
一种适用于在线学习和大规模机器学习的优化算法,主要用于大规模对抗性学习。
Nadam (Nesterov-accelerated Adam):
将 NAG 和 Adam 结合在一起,以尝试获得更快的收敛速度。
4.2损失函数(Loss Function)
损失函数(Loss Function),又称为成本函数(Cost Function)或目标函数(Objective Function),主要用于评估模型预测输出与真实标签之间的差距。它量化了模型在特定任务中的表现,提供了一种度量来指导模型的学习过程。
损失函数的主要功能包括:
评估模型性能:通过计算损失值,损失函数告诉我们模型在给定输入上的预测性能如何。损失值越低,模型的预测效果越好。
优化指导:损失函数为优化算法提供了目标,通过最小化损失函数来更新模型参数,以提高模型性能。
根据具体的任务类型。以下是一些常用的损失函数:
1. 回归任务
均方误差(Mean Squared Error, MSE):\text{MSE} = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2
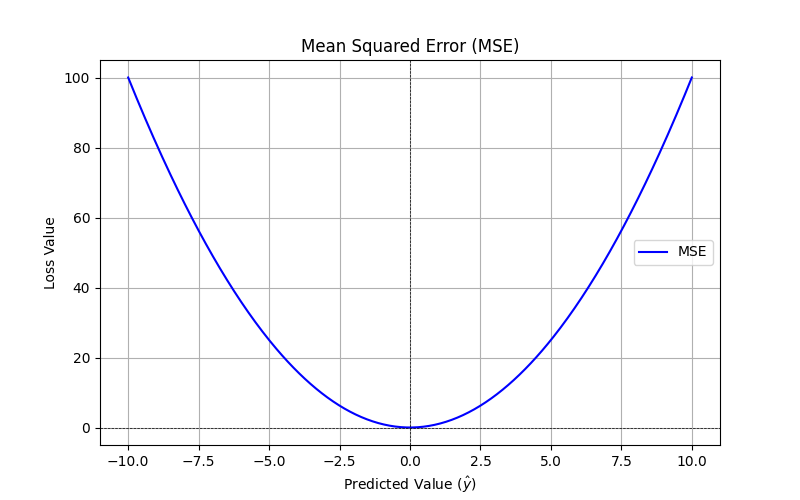
计算预测值与真实值之间的平方差的平均值。适用于回归任务,能够惩罚大的错误。
平均绝对误差(Mean Absolute Error, MAE):\text{MAE} = \frac{1}{n} \sum_{i=1}^n |y_i - \hat{y}_i|

计算预测值与真实值之间绝对差的平均值,对异常值的敏感度较低。
2. 分类任务
二元交叉熵损失(Binary Cross-Entropy):\text{BCE} = - \frac{1}{n} \sum_{i=1}^n [y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i)]
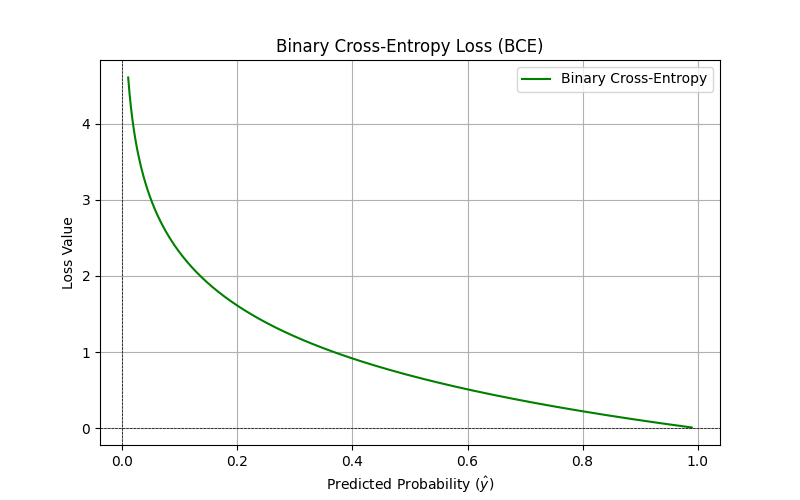
适用于二分类任务,衡量两个类之间的相似性。
多分类交叉熵损失(Categorical Cross-Entropy):\text{CCE} = - \sum_{i=1}^C y_i \log(\hat{y}_i)
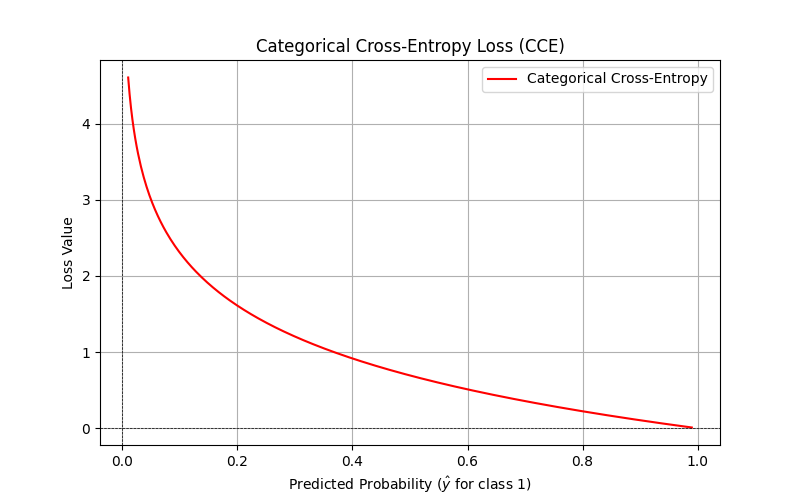
适用于多分类任务,y 是真实的类别分布,C 是类别数。
稀疏分类交叉熵损失(Sparse Categorical Cross-Entropy):
类似于多分类交叉熵,但用于整数形式的标签(即类别索引),常用于多类分类。
4.3评估指标(Evaluation Metrics)
评估指标(Evaluation Metrics)是用于衡量机器学习模型性能的标准或指标。在模型训练和测试过程中,评估指标帮助我们了解模型的效果以及其在实际应用中的表现。选择合适的评估指标对于模型的调优和比较至关重要。
常用的评估指标:
1. 回归任务
均方误差(Mean Squared Error, MSE)\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2:衡量预测值与真实值之间的平方差的平均值。
平均绝对误差(Mean Absolute Error, MAE)\text{MAE} = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i|:衡量预测值与真实值之间绝对差的平均值。
R² 决定系数(Coefficient of Determination, R²)R^2 = 1 - \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{\sum_{i=1}^{n} (y_i - \bar{y})^2}:衡量模型解释数据变异的能力。值在0到1之间,越接近1表示模型越好。
2. 二分类任务
精确率(Precision)\text{Precision} = \frac{TP}{TP + FP}:正确预测为正类的样本占所有预测为正类样本的比例。
召回率(Recall)\text{Recall} = \frac{TP}{TP + FN}:正确预测为正类的样本占所有实际为正类样本的比例。
F1-score:精确率和召回率的调和平均值,适用于类别不平衡的情况。
准确率(Accuracy)\text{Accuracy} = \frac{TP + TN}{TP + TN + FP + FN}:正确预测的样本占所有样本的比例。
3. 多分类任务
多分类精确率、召回率和 F1-score:对每个类别分别计算,通常会用宏平均(Macro Average)或加权平均(Weighted Average)进行综合评估。
混淆矩阵(Confusion Matrix):可视化分类任务的性能,显示模型预测与实际标签的对比。
4. 排序与推荐系统
平均精度(Mean Average Precision, mAP)\text{mAP} = \frac{1}{Q} \sum_{q=1}^{Q} \text{AP}(q):用于评估信息检索和推荐系统的性能,计算不同阈值下的平均精度。
归一化折扣累积增益(Normalized Discounted Cumulative Gain, NDCG)\text{NDCG}@k = \frac{DCG@k}{IDCG@k}:用于评估推荐系统性能,考虑排序和相关性。
5. 其他评估指标
AUC-ROC 曲线(Area Under the Receiver Operating Characteristic Curve)\text{AUC} = \int_0^1 \text{ROC}(t) \, dt:衡量模型分类性能的指标,特别是在二分类中,AUC 值越高,模型性能越好。
对数损失(Log Loss)\text{Log Loss} = -\frac{1}{n} \sum_{i=1}^{n} \left[ y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i) \right]:用于评估概率输出的分类模型,惩罚预测概率与真实标签之间的差距。



